It’s widely accepted/taught that binary search is the fastest way to search sorted lists. It has a worst-case complexity of log2(N), only touching 24 elements for N = 10000000.

However, I recently had the idea that on modern architectures the search time should be dominated by those 24 memory accesses, since they are “random” and will thus not be cached. Based on this, it could make sense to implement an n-ary search, that is one that reads n-1 elements at the same time and finds the interval (within n options) for the next recursive/iterative step. This way, 2-ary search would equal standard binary search, while 3-ary search reads 2 elements per step and decides between the 3 thirds of the search space.

My theory was that this could allow the chip / memory architecture to do the fetches in parallel and mitigate the latency. In the worst case, binary search would use 24 steps, with 24 total, consecutive memory accesses for 10 million elements, while “trinary” search would perform 15 steps, accessing 30 elements but always 2 in parallel. “Quadrary” would require 12 steps, access 36 elements with 3 in parallel, and so on.

I implemented all of those (both recursively and iteratively) and a small testbench which generates N random numbers, searches M other random numbers and repeats the whole measurement R times. Before each search, the cache is cleared by a streaming operation.

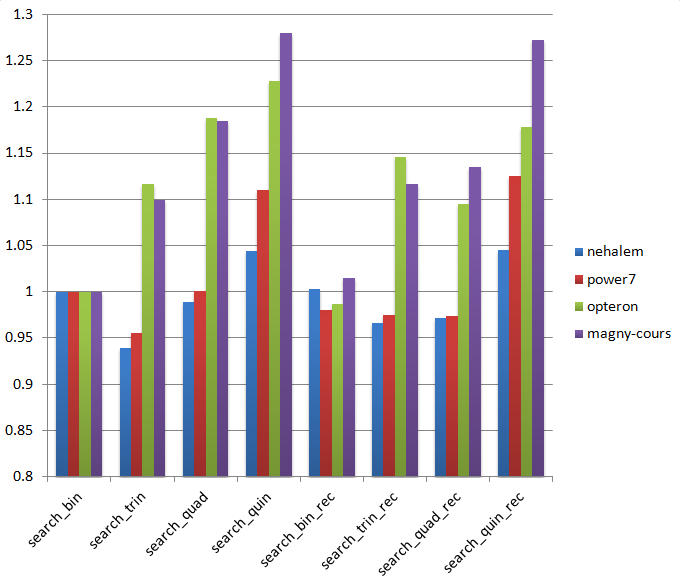
Here are the results on 4 architectures with N=10000000, M=1000 and R=100:

All benchmarks were compiled with GCC 4.6, using -O3 and -march=native. Sadly, the impact wasn’t as large as I would have hoped, but on the nehalem and power7 systems “trinary” search is repeatably 5+% faster than binary search.

Leave a comment if you’re interested in the benchmark code, it’s a bit of a mess right now.